Xem lại bài Toán giúp HS Việt Nam giành giải đặc biệt tại Olympic Toán học quốc tế
Thầy Khánh Trình đã đoạt giải nhất với số điểm tuyệt đối 40/40 đồng thời đoạt giải đặc biệt về lời giải độc đáo trong kỳ thi Olympic Toán học quốc tế, và là học sinh Việt Nam duy nhất đạt giải đặc biệt trong một kỳ thi Toán Quốc tế tính đến nay.
Năm 1979, thí sinh Lê Bá Khánh Trình làm rạng danh Việt Nam khi giành điểm tuyệt đối 40/40 tại Olympic Toán học quốc tế (IMO). Cùng với huy chương vàng, Khánh Trình nhận thêm giải đặc biệt dành cho thí sinh có lời giải đẹp nhất.
Hơn 40 mùa IMO đã qua, thầy Khánh Trình là thí sinh Việt Nam duy nhất có được thành tích này.

Thầy Khánh Trình khi còn trẻ
Bài toán tại Olympic Toán học quốc tế có nội dung như sau:

Đề thi tạm dịch sang Tiếng Việt: Cho hai đường tròn cắt nhau trong một mặt phẳng. Gọi A là một trong các giao điểm của chúng. Có hai điểm, mỗi điểm chuyển động đều trên một đường tròn, xuất phát từ A cùng một lúc theo cùng một chiều. Sau khi đi được một vòng, chúng lại gặp nhau tại điểm A.
Chứng minh rằng có một điểm P trong mặt phẳng sao cho ở bất kỳ thời điểm nào, điểm P luôn cách đều hai điểm chuyển động đã cho.
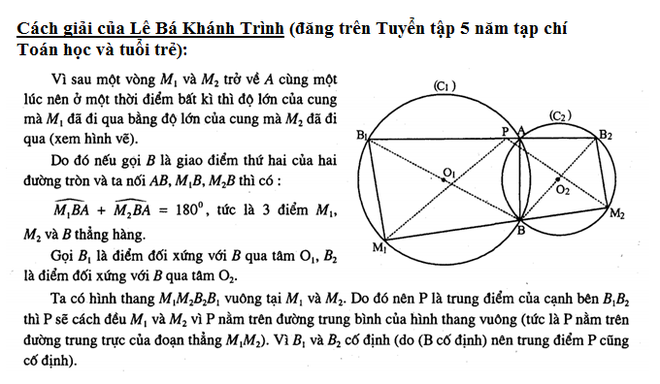
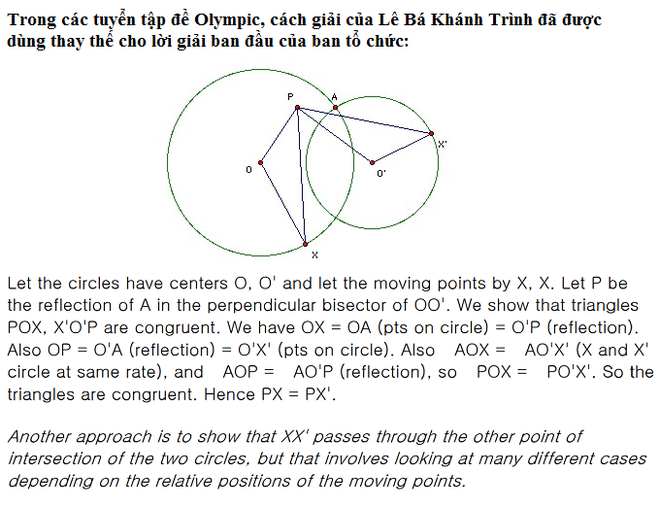
(Nguồn: Tạp chí Toán học và Tuổi trẻ)
Bạn đã thấy nó quá cao siêu, quá kinh khủng so với những gì bạn học ở trường chưa?




