Bí kíp tính nhẩm “bá đạo” khi đi thi quên máy tính
Những mẹo vặt tính nhẩm vừa nhanh vừa chuẩn phục vụ các sĩ tử trong mùa thi cuối năm.
Kể từ khi ra đời, chiếc máy tính bỏ túi đã giúp đỡ con người rất nhiều trong việc giải những bài toán phức tạp. Sử dụng máy tính bạn vừa đỡ mất công, vừa tiết kiệm được một khoảng thời gian so với việc tính thủ công ra nháp.
Tuy nhiên, sử dụng máy tính nhiều lại khiến chúng ta dễ bị phụ thuộc. Lúc này, nếu chẳng may vô tình quên mang theo máy tính, bạn sẽ dễ đầu hàng trước các bài thi ngay lập tức.
Đừng lo, các công thức mẹo dưới đây sẽ là “phao cứu sinh” đắc lực cho bạn. Thậm chí, nếu thành thục chúng, bạn hoàn toàn có thể tự tin đi thi và "cố tình" để quên máy tính ở nhà.
1. Trừ bằng cách cộng
Một điều thú vị mà không phải ai cũng để ý, đó là con người tính nhẩm phép cộng nhanh hơn trừ rất nhiều. Vì vậy, để mọi bài toán trở nên đơn giản, tại sao không biến phép trừ thành cộng cho giản đơn?
Hãy cùng lấy phép tính 1.492 – 1.066 làm ví dụ. Đây là một phép trừ có nhớ nên khiến không ít người cảm thấy khó chịu. Vậy nên thay vì tiếp tục trừ, hãy làm theo các bước sau đây:
Bước thứ nhất, hãy lấy 9 trừ đi các chữ số thuộc số trừ (1.066). Riêng chữ số hàng đơn vị thì ta lấy 10 trừ đi. Kết quả thu được số mới là 8.934.

Bước thứ hai, lấy số vừa mới tạo ra cộng nhẩm với số bị trừ, ta có 8.934 + 1.492 = 10.426.

Cuối cùng, bước thứ ba ta bỏ chữ số đầu tiên của kết quả mới có (10.426), thu được 0426 = 426. Đây cũng chính là kết quả của phép tính ban đầu.

Chúc mừng, bạn vừa biến một phép trừ thành phép cộng trong vài chục giây rồi đó!
2. Tính nhanh bình phương mọi con số
Nếu một ngày đẹp trời, có người đố bạn 77 bình phương là bao nhiêu rồi cho bạn 30 giây suy nghĩ và không dùng giấy bút, bạn sẽ ra sao? Với công thức dưới đây, những tình huống như vậy sẽ trở thành chuyện “nhỏ như con thỏ”.
Bước đầu tiên, hãy tìm số tròn chục (trăm hoặc ngàn) gần nhất với số cần tính bình phương (trường hợp này là 80). Đồng thời ta tính được khoảng cách từ số tròn chục ấy tới số ban đầu (80 – 77 = 3).
Ta kết thúc bước này bằng cách lấy số ban đầu trừ (hoặc cộng nếu số tròn chục nhỏ hơn số ban đầu) đi khoảng cách vừa có (77 – 3 = 74).

Bước thứ hai, nhẩm tính hai số mới có với nhau (74 x 80 = 5.920). Phép tính này hoàn toàn không thể nhầm bởi việc nhân số tròn chục thường không quá khó với tất cả chúng ta.

Bước thứ ba, ta đem cộng kết quả ở bước hai với bình phương khoảng cách (5.920 + 3^2 = 5.929). Đó chính là bình phương ta cần tìm.
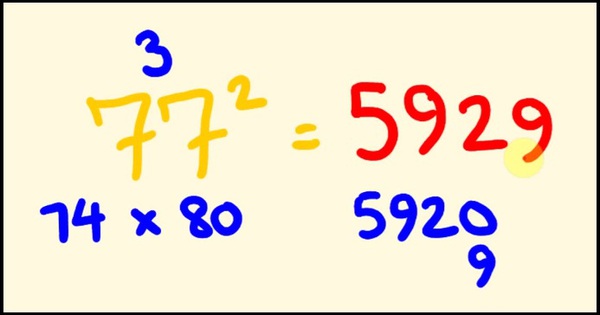
Phương pháp này xuất phát từ một hằng đẳng thức quen thuộc A^2 – B^2 = (A – B) x (A + B). Từ đây, ta suy ra A^2 = (A – B) x (A + B) + B^2.
Theo các nhà toán học, công thức này đúng cho mọi số tự nhiên nhưng chủ yếu nên được áp dụng nhiều nhất với các số có 2 chữ số sẽ đạt được hiệu quả cao nhất.
3. Nhân “siêu tốc” với số có 2 chữ số
Với những phép tính như 21 x 31 hay 99 x 45, bạn có thể tính nhẩm chúng trong thời gian bao lâu? Với cách thức nhân siêu tốc dưới đây, chưa đầy 30 giây là bạn đã giải xong phép tính đó rồi.
Đầu tiên, hãy nhớ rằng mọi phép nhân giữa hai số có 2 chữ số có tích lớn nhất là 9.801 (99 x 99) nên kết quả cần tính có tối đa 4 chữ số.
Sau đó, bước thứ nhất, ta nhân 2 chữ số đầu của hai số với nhau, 2 chữ số cuối với nhau rồi điền vào kết quả cuối cùng (có 4 vị trí dấu “_”). Chẳng hạn với phép tính 21 x 31, ta sẽ được 2 x 3 = 6; 1 x 1 = 1. Ta được kết quả tạm thời là : 6_1
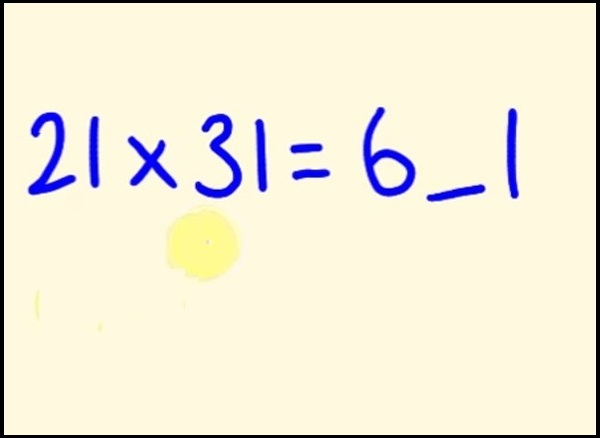
Bước thứ hai, ta lấy chữ số thứ nhất của số thứ nhất nhân với chữ số thứ hai của số thứ hai (2 x 1 = 2), chữ số thứ hai của số thứ nhất nhân với chữ số thứ nhất của số thứ hai (1 x 3 = 3).

Cuối cùng, bước thứ ba, ta cộng hai số với nhau và điền vào dấu “_” ở giữa (2 + 3 =5), được kết quả là: 651. Dấu “_” còn lại trong trường hợp này sẽ không được điền và ta có tích cần tính.

Vậy đối với các số lớn hơn thì sao? Về bản chất, thủ thuật không thay đổi, nhưng bạn cần linh hoạt hơn. Chẳng hạn 99 x 45. Áp dụng bước 1, ta được kết quả 3.645.
Sau đó với bước 2, ta thu được số 81 (9 x 4 + 9 x 5). Lấy 1 + 4 = 5, ta được chữ số hàng chục của kết quả cuối cùng.
Bước 3, ta lấy 8 cộng với 36 được 44. Vậy kết quả cuối cùng sẽ là 4.455.
Thực tế, đây chính là phương pháp khai triển theo chiều ngang của phép nhân thông thường học ở trường, nhưng ưu điểm của nó là giúp bạn thấy bài toán một cách trực quan hơn, từ đó có thể tính nhẩm kết quả một cách dễ dàng.
Các bạn thấy những mẹo vặt tính nhẩm trên thế nào? Hãy áp dụng thử và nêu cảm nhận của mình bằng cách comment dưới đây nhé!
Nguồn: Sciencealert, Tecmath
TIN CÙNG CHUYÊN MỤC
Xem theo ngày
